はじめまして.大阪大学大学院 理学研究科 修士2年の井元宏明と申します.私は培養細胞を用いた実験と数理モデリングを合わせて,細胞運命決定のメカニズムについて研究しています.
ここで改めて「運命決定」というものについて考えるために,「オペラ座の怪人」より,”Down Once More”の歌詞を引用したいと思います.この場面では,ファントム(怪人)が歌姫クリスティーヌに大きな決断を迫ります.
Refuse me, and you send your lover to his death!
https://genius.com
This is the choice—
This is the point of no return!
この”Point of No Return“とは「もはや後に引けない段階」という意味です.運命を決めるといったような重大な決断を行う際にはしばしば,”Point of No Return“を超えなくてはなりません.そして,それは細胞も同じです.
実は,私たちのからだを構成しているひとつひとつの細胞それぞれが,増殖するのかしないのか,生きるのか死ぬのかという重大な運命決定を,外界からの情報をもとに自分で行なっています.
細胞は増殖したい気持ちを持ちながらも,一方で傷のある遺伝情報を次世代に残すことは深刻な問題を引き起こしかねないので,大人しくしておいたほうがいいのでは,とも考えています.しかし,いつかは自身の運命を決めなくてはなりません.
私の研究は,そんな悩める細胞の”Point of No Return“がどのような分子メカニズムによって制御されているかを明らかにしようとするものです.
この記事を通じて,数理科学が生命科学とどのように関わっているのか,そして,こうした学際分野の研究の面白さを感じていただけたらと思います.
目次
細胞運命は一度決めたら戻れない
細胞は,ホルモンや成長因子,神経伝達物質のような外部からの刺激(情報)を受け取り,適切に応答することが不可欠です.例えば,傷の治癒のために増殖したり,神経系の構築のために分化したり,時には,新陳代謝のために死ぬことも必要です.
ところで,細胞が感知しなければならない情報というのは決して単純明快なものではありません.なぜなら,細胞内外の環境は絶え間なく変化しているからです.しかしながら,そうした「ゆらぎ」にいちいち呼応していたら,いつまでも適切な運命決定ができません.
したがって,細胞には,例えば一度増殖すると決めたら,たとえ環境が増殖に不利な方向に変化しても,その決定を覆さないような不可逆的な運命決定を制御するシステムが必要になります.
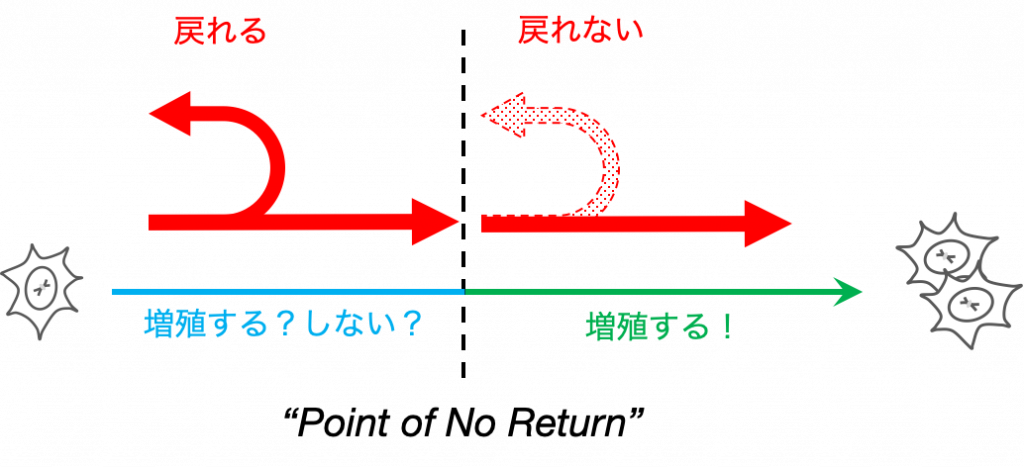
次に,環境からの情報を細胞内に伝えるシグナル伝達経路と,細胞運命の中でも細胞増殖と密接に関連する,細胞周期の不可逆性の制御について説明します.
シグナル伝達と不可逆的な細胞周期制御
シグナル伝達経路
細胞は,外部からの刺激に応答して適切な運命決定を行うために,シグナル伝達経路を介して情報を伝達します.シグナル伝達経路は非常に多くのタンパク質の複雑な相互作用により構成されるネットワークです.
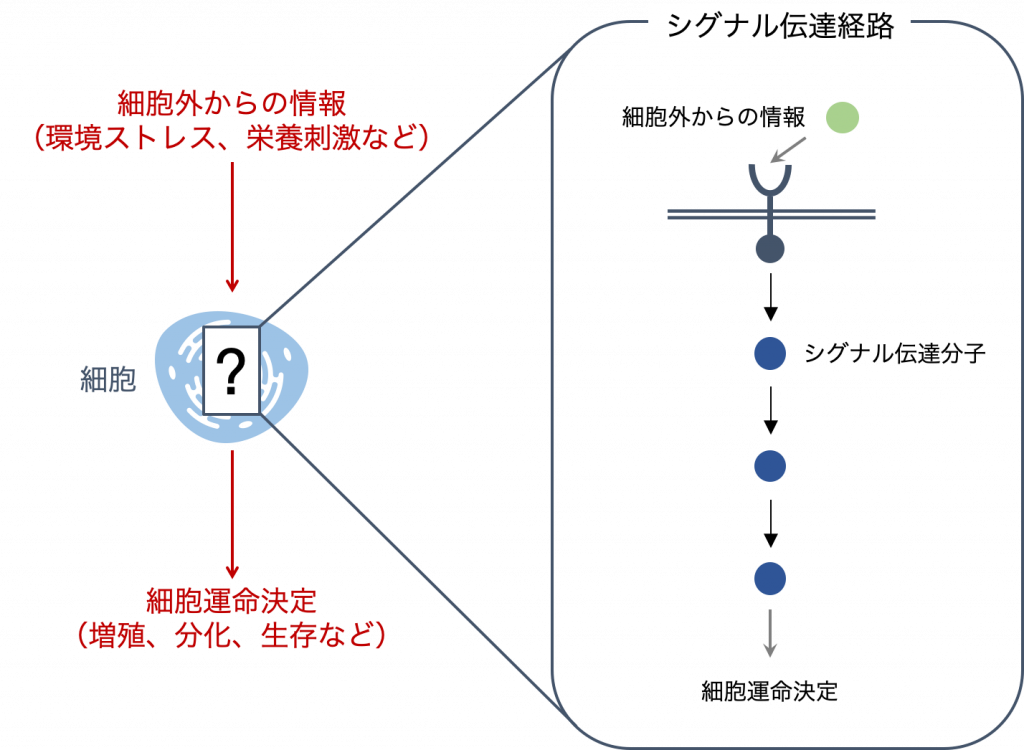
細胞外からの情報(入力)は,細胞膜表面で受容されたのち,シグナル伝達分子のリン酸化などを介して伝言ゲームのようにリレー形式で細胞内へと伝達され,増殖・分化・生存といった運命決定へと出力されます.
興味深いことに,細胞は「増殖・分化」といった異なる細胞応答を共通したシグナル伝達経路の活性化から生み出すことができます.では何が,細胞応答の違いを引き起こしているのでしょうか?
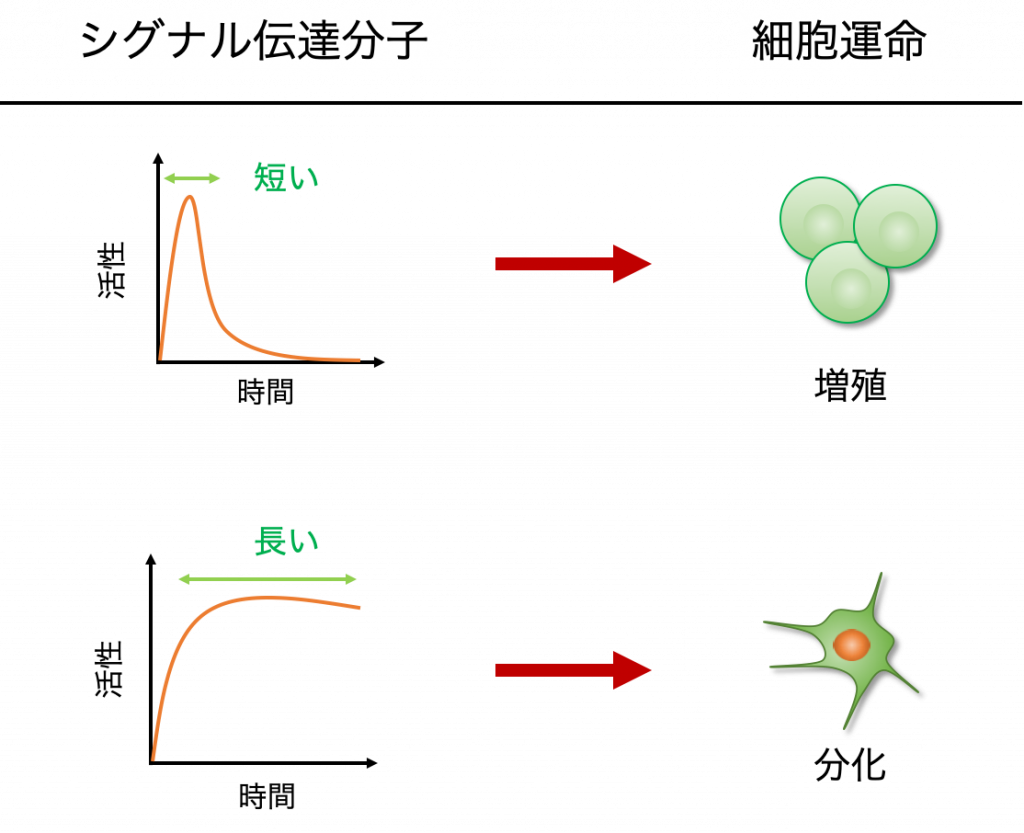
こうした異なる細胞応答には,シグナルのダイナミクスの違い,つまり,シグナル伝達分子の活性の強弱や,それが長く続くのか,あるいはすぐに活性が低下するのかといった情報が重要であるということがわかっています.
例えば,PC12という神経細胞のモデル細胞では,ERKというタンパク質の活性の持続時間が短い時は増殖を,長い時には分化を誘導することが知られています.
シグナル伝達経路にはこのように,活性の持続時間の違いのようなアナログな情報を,最終的には「分化するか・しないか」のようなデジタルな情報に変換する高度なシステムが備わっています.
細胞増殖の運命決定は慎重に
細胞周期は,1個の細胞が2個に分裂するまでの一連の反応過程で,形態学的な分類からG1, S, G2, Mの4つのフェーズに分けられます.細胞増殖のためには,この細胞周期の進行が不可欠になります.
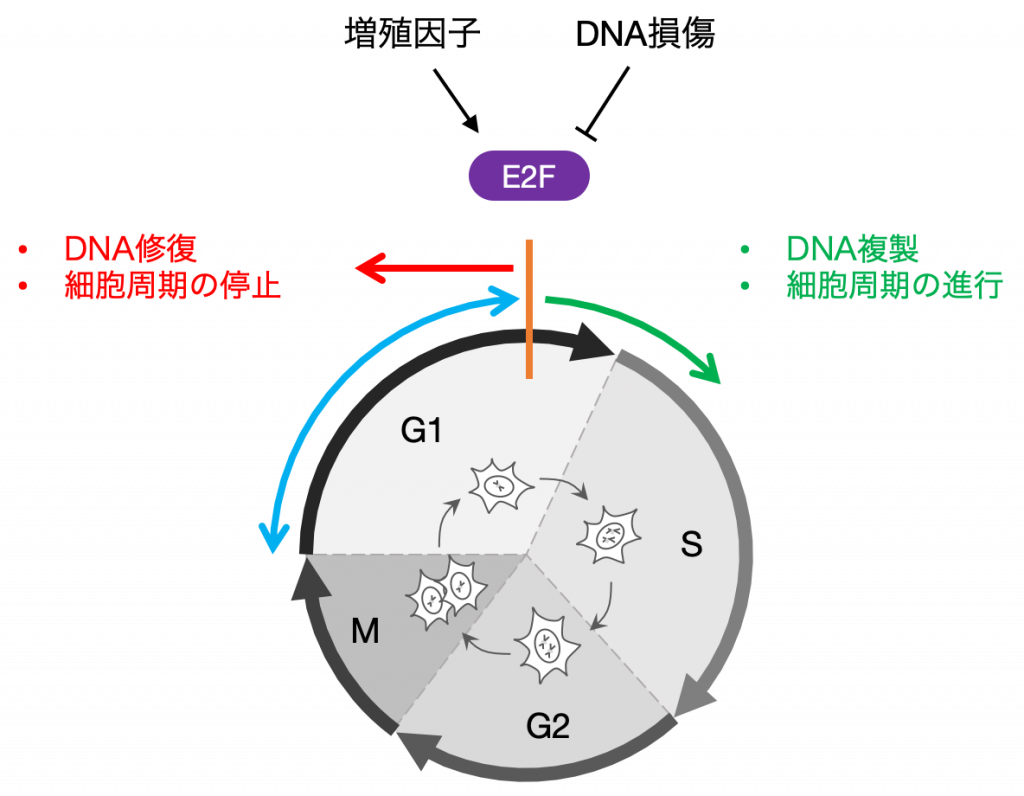
細胞は,外部の増殖因子により刺激を受けると,細胞増殖のために必要なタンパク質が作られ,細胞周期の進行を促進します.一方で,細胞は常に熱,放射線,化学物質等に曝されており,それらによってDNAに傷がつけられます.
DNAには遺伝情報の全てが記されているので,冒頭にも述べたようにDNA損傷を放置したまま次代に遺伝情報を受け渡すことは,細胞のがん化などの深刻な問題を引き起こす要因となります.したがって,細胞は時として,DNA損傷を修復するために細胞周期を停止することも必要になります.
しかし,細胞は「細胞周期を進行させるか,停止させるか」いつまでも迷っていることはできません.細胞周期のある時点を超えると,細胞は内外の情報を統合して,不可逆的な運命決定を行い,DNA複製を開始します.
この運命決定において重要な働きをするのが,次に紹介するE2Fと呼ばれる転写因子です.
細胞増殖を司る転写因子E2F
まず,転写因子とは何かを説明します.
DNAに記された遺伝情報はRNAに転写され,タンパク質に翻訳されてその機能が発現します.この分子生物学の基本原則をセントラルドグマと呼びます.転写因子は,DNAの特定の領域に結合し,RNAへの転写の過程を促進,あるいは逆に抑制する,細胞内の反応において重要なタンパク質です.

転写因子E2Fは細胞周期の進行に必要な一連の遺伝子群の発現を制御し,細胞増殖に必須の役割を果たしています.
E2Fは,増殖因子の量を増加させて一度活性化すると,その後増殖因子を除いても不活性化されないという不可逆的な応答を示します.
私の研究目的は,このE2Fの不可逆的な応答に,シグナルのダイナミクスが及ぼす影響を明らかにすることです.
ここまでの説明でお分かりいただけるように,シグナル伝達経路や細胞周期には複雑な制御機構が備わっています.こうした制御様式を理解するためには,実験研究だけではなく,数理科学的なアプローチが大変有効です.
それでは次に,私の具体的な研究内容を説明します.
シグナル依存的な細胞周期制御の解明に向けて
数理モデルの構築
数理モデルは,様々な現象を数式によって表現したもので,それによって現象の性質をより深く理解できるようになります.今回私はまず,細胞内で起こる反応を数式で表すことを試みました.
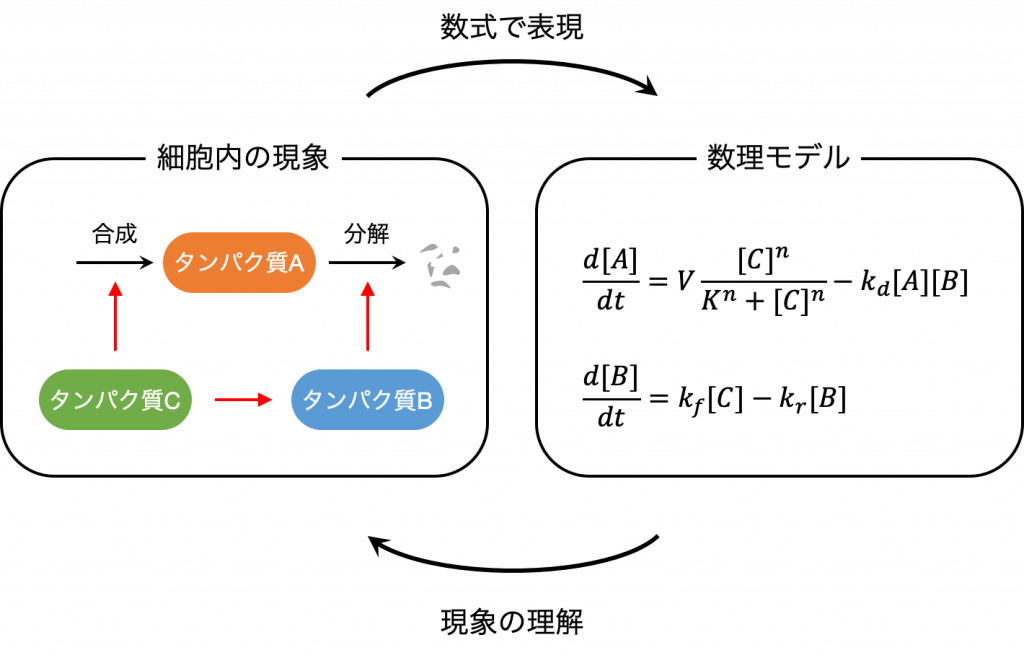
細胞内で起こる生化学反応の反応速度は,反応に関わる分子の濃度の関数として比較的簡単に記述できます.
「微分」を用いると,単位時間あたりの濃度の変化量をみることができます.そこで,細胞内の1反応に注目するのではなく,複数の反応ネットワークを1つの「かたまり」として捉えることで,反応過程に関わる分子の濃度変化をそれぞれ反応速度論に基づいた微分方程式により記述することでモデル化します.
構築した微分方程式モデルは,分子の濃度が時間の経過とともにどのように変化するのかを予測したり,注目する分子の挙動に最も影響を与える化学反応がどれかを調べたりすることに利用できます.
まず私は,細胞が外界からの刺激を受容し,細胞内シグナル伝達経路を活性化し,細胞周期制御に入るまでの一連の反応過程を微分方程式により記述しました.
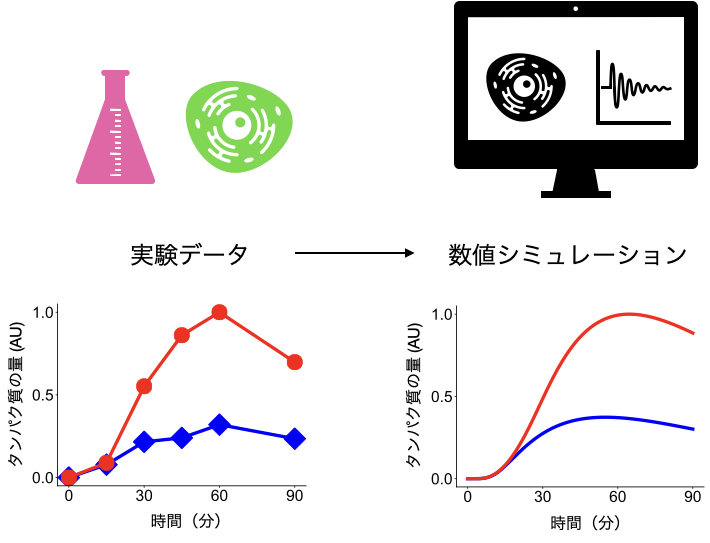
数理モデルを実験系の評価・解析・予測に使用するには,モデルがきちんと実験結果を反映していることが必要になります.そこで,次に私は,実験データを数値シミュレーションによって再現することを目指しました.
今回は,異なる成長因子で刺激した際のシグナル伝達分子の活性化パターンを実験で取得し,数理モデル内のパラメータの値を最適化して実験データを再現しました.
どうやってモデルの解析をするのか
次に,構築した数理モデルをどのように解析するかを説明します.ここでは,細胞周期が進む or 進まないという事象を,数理の言葉で表現することを目指します.
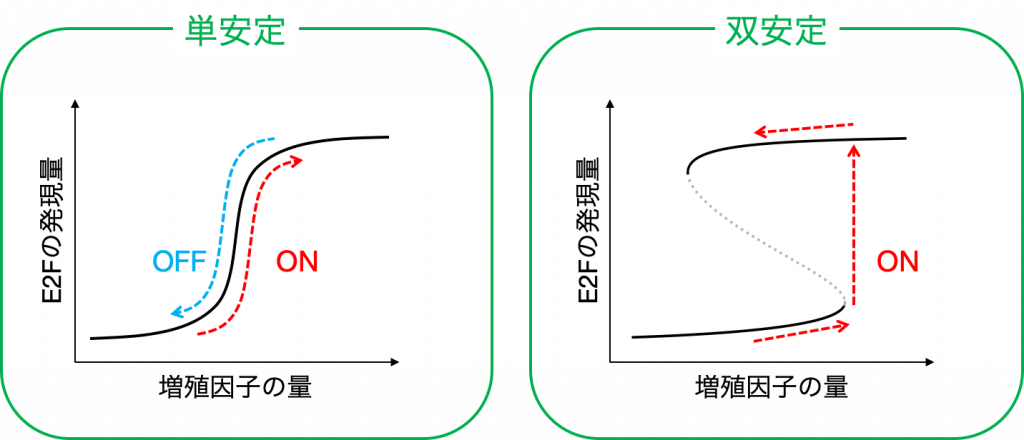
まず,モデル内で増殖因子の量を増加させながら,細胞周期の進行の指標となるE2Fがどのように応答するかを調べていくと,ある増殖因子のレベルを境に急激に活性化されることがわかります.そして,この活性化の様式は「単安定」,「双安定」の2種類に分類されます.
「単安定」の場合は,たとえE2Fが一度活性化されても,その後増殖因子の量が減ってしまうとすぐに不活性化されてしまいます.
一方で「双安定」の場合は,たとえ活性化した後に増殖因子の量が減少しても,E2Fの発現量は減少することなく,高いレベルを保ち続けることができます.そして,この双安定な領域が広いほど,増殖因子の変動の影響を受けづらいことを意味します.
シグナル伝達分子のダイナミクスが細胞周期制御に及ぼす影響の予測
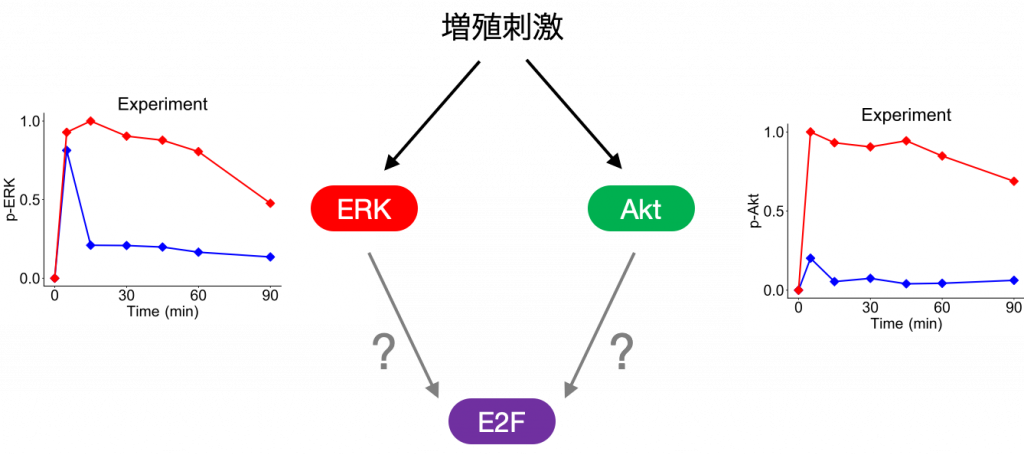
最後に,上記の解析を構築したモデルに適用した結果について説明します.今回は,シグナル伝達分子として,細胞運命決定を制御する生体内で広く発現・機能しているERKとAktの2つのタンパク質のダイナミクスに注目しました.
本研究で実験に用いたヒト乳がん由来のMCF-7細胞はEGFという成長因子で刺激すると,ERKは一過的な活性化のダイナミクスを示し,HRGという別の成長因子で刺激すると活性が持続的になります.
一方,AktはEGF刺激では活性の強度(ピークの最大値)が低く,HRG刺激では高くなります.つまり,ERKとAktは,2種類の成長因子による刺激により異なる応答を示します.
今回は,シグナル伝達分子の活性化パターンを数値シミュレーションにより変化させて,E2Fの発現量に及ぼす影響を解析しました.
その結果,
- ERK活性の持続時間が短いとE2Fは発現されず,ある一定の持続時間を越えると発現される
- Aktの活性化強度はE2Fの発現量には影響しないが,強度が弱くなると双安定領域が狭くなり,最終的には単安定になる.つまり,不可逆性の制御と関連する
以上2つの結果が得られました.
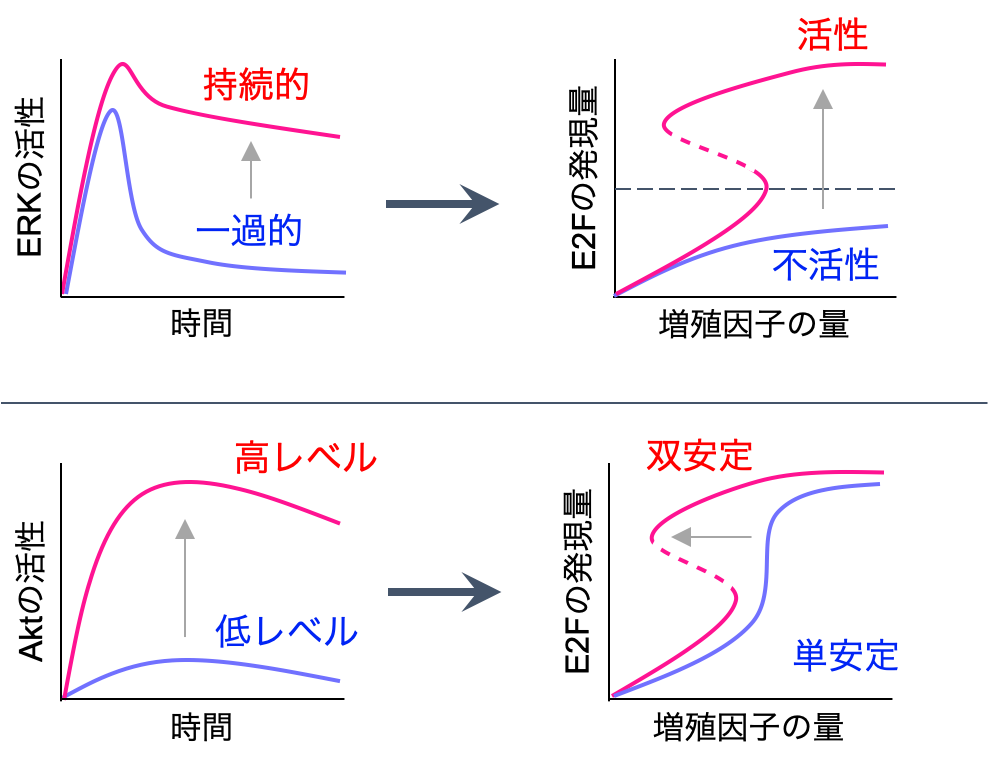
数理モデルを用いた解析結果から,これら2つのタンパク質は,それぞれ異なる作用機序で細胞増殖に重要な役割を果たしていることが示唆されました.
今後は,今回得られた解析結果を,ERK, Aktそれぞれの阻害剤を用いて実験的に検証します.数理モデルによる予測と実験検証を繰り返し,シグナル伝達系の定量的な細胞周期制御を明らかにしていきたいと考えています.
終わりに
私が学部で入学したのは生物科学科ですが,実験を除く講義のほぼ全ては,数学と物理の授業を選択していました.
そのような,生物学とは一見関連がなさそうに見える分野の勉強に没頭していた理由は,「いつか数理科学的な素養が生物の研究で役に立つかもしれないから」という打算的な思惑があったからではありません.実利的な側面を意識する以前に,非常に魅力的でした.
そして現在の研究の支えになっているのは,分野にかかわらず,純粋な知的好奇心に導かれて修得した知識・技術です.「今勉強していることが将来なんの役に立つか」なんて,そんなことはわからないものです.
これは大学院生として,中高生・大学の学部生に確信を持って言えることですが,今皆さんが勉強している内容で無駄なことなんて何一つありません.「面白いな,もっと知りたいな」という気持ちを忘れずにいて欲しいです.
そして,勝手な思い込みや安易な判断に流されず,「物事を突き詰めて考え,理解する」という姿勢を大切にしてください.そういった経験の積み重ねによって獲得した知識は今後,たとえ直接的な形で活かされなくても,皆さんにとってかけがえのない財産となるはずです.
最後までお読みいただきありがとうございました.研究内容・この記事に関するお問い合わせは以下よりお願いいたします.
- Email: himoto@protein.osaka-u.ac.jp
参考文献
- Santos, S. D. M., Verveer, P. J. & Bastiaens, P. I. H. Growth factor-induced MAPK network topology shapes Erk response determining PC-12 cell fate. Nat. Cell Biol. 9, 324–330 (2007).
- Yao, G., Lee, T. J., Mori, S., Nevins, J. R. & You, L. A bistable Rb-E2F switch underlies the restriction point. Nat. Cell Biol. 10, 476–482 (2008).
- Nakakuki, T. et al. Ligand-specific c-Fos expression emerges from the spatiotemporal control of ErbB network dynamics. Cell 141, 884–896 (2010).
- Barr, A. R., Heldt, F. S., Zhang, T., Bakal, C. & Novák, B. A Dynamical Framework for the All-or-None G1/S Transition. Cell Syst.2, 27–37 (2016).
- Heldt, F. S., Barr, A. R., Cooper, S., Bakal, C. & Novák, B. A comprehensive model for the proliferation–quiescence decision in response to endogenous DNA damage in human cells. Proc. Natl. Acad. Sci. 115, 2532–2537 (2018).
- Imoto, H. & Okada, M. Signal-dependent regulation of early-response genes and cell cycle: a quantitative view. Curr. Opin. Syst. Biol. 15, 100–108 (2019).