こんにちは。高橋 和音 (Kazune Takahashi) と申します。現在は、東京大学大学院 数理科学研究科で特任研究員をしております。この記事では、変分法の概説を試みます。変分法は、微分方程式を考察する代表的な手法です。自己紹介がわりに、どうして変分法を専門にしたのかまず話したいと思います。
私は、大学の数学を勉強し始めてから、積分の世界の素晴らしさに魅了されました。
高校までですと、積分は原始関数を介して求めます。ところが、大学以降に勉強する高度な手法を使うと、例えば原始関数が書けない関数の定積分の正確な値が求まるケースがあります。また、正確な値を求めることができずとも、ある値よりも小さい or 大きいことが分かることが重要である場面も増えてきます。そういう一連の手法が好きになりました。
以下で「汎関数」が出てきますが、変分法で使う汎関数は、関数の積分で書かれます。変分法は、積分を取り扱うのが好きな私には合っている研究対象だと思っています。
まず最初は微分方程式の話をします。微分方程式を取り扱う上で重要な手法として、変分法があります。そこでこの記事では変分法の話をします。
変分法を述べるために必要な言葉は、「臨界点」「汎関数」の 2 つです。微分方程式の導入に続いて、順番に見ていきます。
「臨界点」は、実は高校生でも \( 1 \) 次元の場合を取り扱っている身近な対象です。これに続く形で、大学 1 年生で多次元の場合を取り扱います。そして、実は、変分法では、無限次元の場合を取り扱うのです。
無限次元といきなり言われてもピンとこないかもしれません。そこで、無限次元空間である「関数空間」について、高校生でも計算できる具体例を挙げてお話しします。無限次元空間が存在することに親しみを持ってくださると思います。すると「汎関数」の定義ができ、「変分法」について概説できるようになります。こういう流れで進めていきます。
導入
皆さんは微分方程式と聞くと、何を思い浮かべるでしょうか。
「方程式とは、解を求めるものだ」ということは、中学校以降のイメージとしてあるでしょう。高校の数学 III の教科書の最後には、簡単な微分方程式が発展項目として出てきていますから、具体的なイメージが湧く方もいらっしゃるかもしれません。
この記事では、変分法について、その主となるアイデアをお話ししたいと考えております。変分法は、微分方程式を本格的に取り扱うための重要な手法の 1 つです。そのためにまず、微分方程式について少し説明します。
微分方程式の導入
微分方程式は、関数方程式の一種です。関数方程式とは、関数を解として求める方程式のことです。
関数方程式は、それ自体は抽象的なものではありません。高校の教科書や大学入試問題でも取り扱われます。その一例が「以下を充たす多項式 \(f\) を求めよ」というものです。 \( f(1) = 1 \) 及び
\[ x \int _ 1 ^ x f(t)dt = (x – 2) \int _ 1 ^ {x + 1} f(t) dt. \]
これは高校の数学 II 程度の知識で解けます(ちなみに答えは \( f(x) = -2x + 3 \) です)。これは関数方程式の例です。この場合、方程式に積分が登場しているので、積分方程式と言います。
ですから、微分方程式というのは、方程式に微分が登場している関数方程式のことです。現行の高校の数学 III の教科書の発展課題として、微分方程式が載っていると思います(載っていない教科書もあります)。それを読んでみるといいかもしれません。
多変数関数とその微分
高校で取り扱われる微分は、すべて \( 1 \) 変数関数についての微分でした。ところで、微分方程式は、自然科学のたくさんの分野で、状態や変化を記述するために、広く応用があります。その場合、変数を増やす必要性が出てきます。
例えば私たちが住んでいる空間は \( 3 \) 次元空間ですから、そこで起こる現象の記述には、 \( 3 \) 変数が必要になるでしょう。さらに、時間の変化も考えることも自然です。すなわち、もう \( 1 \) 変数加わるので \( 4 \) 変数が必要になるでしょう。この他にも様々な理由で変数が増え、一般に \( N \) 変数関数を取り扱う必要があります。
こうすると、高校の数学 III で導入する微分では道具としては物足りなくなります。そこで大学 1 年生の微分積分では方向微分を定義します。これは \( N \) 次元空間で、ある方向に沿って微分を考えるというものです。
そのうち特に重要な「方向」として、「ある一つの変数だけ動かす。しかし他の変数は動かさない」という「方向」があります。これを偏微分といいます。
そして、偏微分を含む方程式を、偏微分方程式といいます。逆に \( 1 \) 変数関数の微分方程式を常微分方程式といいます。これらはどちらも重要な研究対象で、どちらも重要な結果を他分野に与えています。
偏微分方程式は難しい
さて、大学生だと、微分方程式を解析的 or 数値的に解く機会が、勉強していくうちにあると思います。大学 1 年生の理科の講義や、大学 2 年生の数学の講義で、パターン別の常微分方程式の解法や理論も勉強すると思います。
しかし、専門数学で扱う偏微分方程式のほとんどは、少し難しくなるだけで、何にもわからなくなります。解が存在するのか、それとも存在しないのかということすら、簡単にはわからなくなるのです。
そこで、大学の学部 4 年生や大学院以降に勉強する高度な手法を使って、研究を進めます。または高度な手法を新たに整備して、新しい微分方程式を調べます。
微分方程式を調べるための代表的な手法が変分法です。以下、変分法の概説をします。
臨界点について
高校や大学 1 年生の数学での「臨界点」
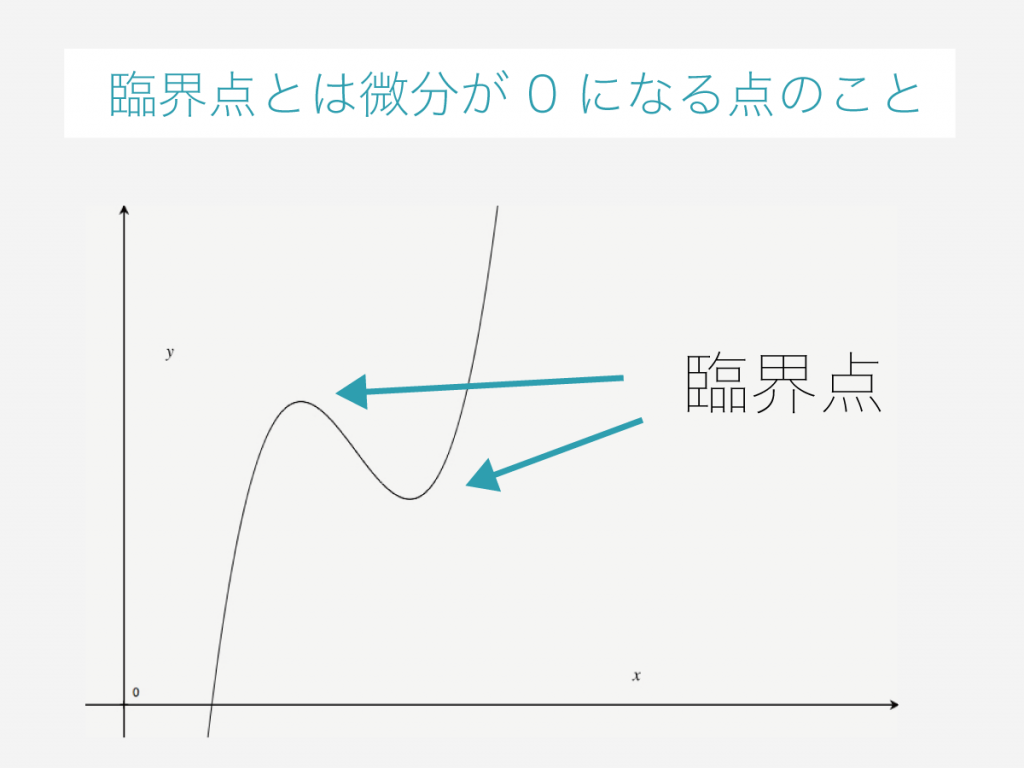
変分法というのは、結局何をしているかというと、臨界点を求めるということです。臨界点というのは、微分が \(0\) になる点のことです。
微分が \( 0 \) になる点を求めるというのは、高校の数学から馴染みのある計算でしょう。高校の数学 III では、関数の微分をして、微分が \( 0 \) になる点を求め、極大点・極小点を求めることをよくやると思います。増減表をかいて、グラフをかく練習をするでしょう。
そして大学 1 年生になると、多変数関数の微分法を勉強します。要するに、高校の数学 III までは \(1\) 次元であった定義域を、 \(2\) 次元以上に拡張したものの微分を習います。
ここで重要なことは、変数が \(2\) つ以上になると、臨界点を求めるというのは、極大点・極小点を単純に求めるということではないということです。
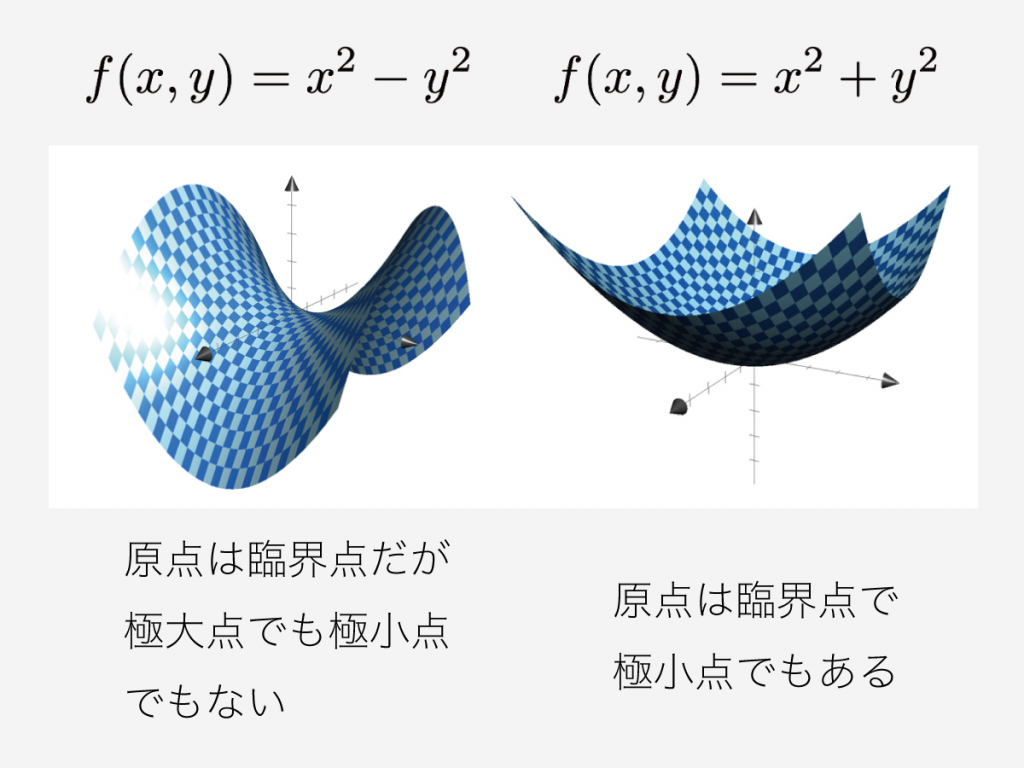
話をわかりやすくするために、まず \(2\) 変数関数の極小点の例をお見せしましょう。 \(2\) 変数関数 \(f(x, y) = x^2 + y^2\) の原点 \((0, 0)\) は極小点です。そして臨界点でもあります。
しかし、臨界点ではあるが、極大点でも極小点でもないという例があります。例えば \(2\) 変数関数 \(f(x, y) = x^2 – y^2\) の原点 \((0, 0)\) は、臨界点ではありますが、極大点でも極小点でもありません。この形状をよく「馬の鞍の形をしている」と言われます。
ですから大学 1 年生では「多変数関数では、偏微分が \(0\) になる点だからといって極大点・極小点だとは簡単にはわからないのだよ」と啓蒙されます。
よく考えると高校の数学 III の段階でも、微分が \(0\) になったとしても極大点でも極小点でもない点というのがありました。 \(f(x) = x^3\) の \(x = 0\) の点などです。
このことは後半で重要になるので、記憶しておいてください。
ユークリッド空間から関数空間へ
「臨界点」については、高校・大学 1 年生の数学でも取り扱われることを見ました。続けて「汎関数」の説明をしたいと思います。汎関数とは、定義域が「関数空間」である関数のことです。
すなわち、以下のようなことです。今まで、私たちは \(N\) 次元ユークリッド空間を定義域に持つ関数 \(f\) を微分して、 \(f\) の臨界点を求める話をしてきました。ここで、その定義域を、ユークリッド空間から関数空間 \(H\) に置き換えようと思います。
関数空間について
関数空間は大学 3・4 年生で講じられる内容です。正確に説明するのは難しいです。しかし、
- 多くの関数空間は無限次元空間であるということ
- 性質の良い関数空間には内積が入ること
については、ここで概説したいと思います。
内積の記号
まず記号の使い方を規約します。高校の教科書でベクトルの内積は \(\vec{v} \cdot \vec{w}\) のように \(\cdot\) を用いて表記していると思います。
これももちろん一般的な記号の使い方ですが、大学以降は \((\vec{v}, \vec{w})\) のように \((,)\) を用いて表記するのがより一般的です。これを使用します。
関数空間の内積の例
実は高校生でも、関数空間について、実質的にはエッセンスに触れています。その例を紹介するために、関数空間 \(L^2[0, 2\pi]\) について述べます。
定義: \(L^2[0, 2\pi]\) とは、以下の条件を充たす区間 \([0, 2\pi]\) 上の関数 \(f\) 全体の集合であると定義する。
\[ \int _ 0 ^ {2\pi} |f(x)|^2 dx < \infty. \]
関数空間 \(L^2[0, 2\pi]\) で以下の内積が定義される。
\[ (f, g) _ {L^2 [0, 2\pi]} = \int _ 0 ^ {2\pi} f(x) g(x) dx. \tag{1} \]
高校生が (1) を見ても、これが内積だといきなり納得してくれるのは無理があるかもしれません。しかし (1) は高校の数学で扱う普通のベクトルの内積と全く同じ性質を充しています。以下そのことを見てみましょう。
まず任意のベクトル \(\vec{v}, \vec{w}\) に対し、
\[ (\vec{v}, \vec{w}) = (\vec{w}, \vec{v}) \]
が成立しますが、任意の \(f, g \in L^2[0, 2\pi]\) に対し、
\[ (f, g) _ {L^2 [0, 2\pi]} = (g, f) _ {L^2 [0, 2\pi]} \]
が成立します。 (1) の定義に照らし合わせれば明らかですね。
また、任意の実数 \(a, b\) と任意のベクトル \(\vec{u}, \vec{v}, \vec{w}\) に対し、
\[ (a\vec{u} + b\vec{v}, \vec{w}) = a(\vec{u}, \vec{w}) + b(\vec{v}, \vec{w}) \]
が成立しますが、やはり任意の実数 \(a, b\) と任意の \(f, g, h \in L^2[0, 2\pi]\) に対し、
\[ (af + bg, h) _ {L^2 [0, 2\pi]} = a(f, h) _ {L^2 [0, 2\pi]} + b(g, h) _ {L^2 [0, 2\pi]} \]
が成立します。これも積分の性質として高校で習います。
また、任意のベクトル \(\vec{v}\) に対し、
\[ (\vec{v}, \vec{v}) \geq 0\]
が成立しますが、任意の \(f \in L^2[0, 2\pi]\) に対し、
\[ (f, f) _ {L^2 [0, 2\pi]} \geq 0 \]
が成立します。これも (1) の定義よりすぐわかります。
最後に、任意のベクトル \(\vec{v}\) に対し、
\[ (\vec{v}, \vec{v}) = 0 \Longleftrightarrow \vec{v} = 0\]
が成立します。同様に、任意の \(f \in L^2[0, 2\pi]\) に対し、
\[ (f, f) _ {L^2 [0, 2\pi]} = 0 \Longleftrightarrow f = 0 \tag{2} \]
は、ちょっと怪しいですけど、成立すると思っていただいて結構です。例えば\(f\)が連続関数なら、確実に成立しています。
以上のことを鑑みると、 (1) は内積のような気がしてきませんか? 少なくとも、普通の内積と同じ式変形が可能であるから、内積だと思って普通に計算して良いということは、納得していただけると思います。

補足
大学 1 年生で線形代数を勉強すると、線形空間上で内積を一般的に「定義」します。今確かめたことで (1) はその「一般的な内積」であることが「証明」されます。だから大学 1 年生以降は、 (1) は、一般的な内積の例と理解することになります。
あと、詳細は省きますが、高校や大学 1 年生までの数学では、厳密には実は (2) は不成立です。これは積分がリーマン積分であることが根本的な問題になっています。これを解決するためには大学 3 年生でルベーグ積分を導入し、\(L^2[0, 2\pi]\)の定義を細工することになります。すると (2) は成立するようになります。
もう一つ補足しておきますと、大学 1 年生以降では、複素数値で内積を扱うことが増えます。この場合 (1) の\(f, g\)の片方の複素共役をとるのが正しいです。すなわち、流儀が 2 つあります。その 2 つは、異なるものですが、どちらの流儀も現実世界では使用されています。
高校生で扱う例
高校 3 年生になると大学入試に向けて問題集を解くと思います。その中で、次の結果は大体の人は触れると思います。
命題: \(m, n\) を自然数とする。次式が成立する。
\[ \begin{align} \int _ 0 ^ {2\pi} \sin mx \sin nx dx &= \begin{cases} \pi & (m = n), \\ 0 & (m \neq n), \end{cases} \\ \int _ 0 ^ {2\pi} \cos mx \cos nx dx &= \begin{cases} \pi & (m = n), \\ 0 & (m \neq n), \end{cases} \\ \int _ 0 ^ {2\pi} \sin mx \cos nx dx &= 0. \end{align} \]
この命題は、実際に高校の数学 III の知識で計算して確かめることができます。
これを (1) の定義で書き換えましょう。すると、上記命題は以下のように書き換えることができます。
命題: \(m, n\) を自然数とする。次式が成立する。
\[ \begin{align} (\sin mx, \sin nx) _ {L^2 [0, 2\pi]} &= \begin{cases} \pi & (m = n), \\ 0 & (m \neq n), \end{cases} \\ (\cos mx, \cos nx) _ {L^2 [0, 2\pi]} &= \begin{cases} \pi & (m = n), \\ 0 & (m \neq n), \end{cases} \\ (\sin mx, \cos nx) _ {L^2 [0, 2\pi]} &= 0. \end{align} \]
このうち、特に、右辺が\(0\)になっている部分に注目してください。これは関数が直交していることを意味しています。
こう書くとわかる通り、無限個の関数の集合 \(\{ \sin nx, \cos nx \} _ {n = -\infty} ^ \infty\) の異なる元は直交していることになります。もちろん (1) の内積の意味で、です。
無限次元空間
この事実をよく考えてみましょう。いわば、人間の感覚を超越していることが起きていることに気づくでしょう。
例えば \( 2 \) 次元平面で、 \( 3 \) 個以上からなる異なるベクトルの集合の任意の \( 2 \) つの元が直交することはあり得ません。同様に \( 3 \) 次元空間で、 \( 4 \) 個以上からなる異なるベクトルの集合の任意の \( 2 \) つの元が直交することはあり得ません。
ところがいま、無限個からなる集合 \(\{ \sin nx, \cos nx \} _ {n = -\infty} ^ \infty\) の任意の \(2\) つの元は、直交しています。
ゆえに、こういう状態が起こるためには、そもそも「空間が無限次元である」としか考えられません。そして実際その通りで、関数空間 \(L^2[0, 2\pi]\) は無限次元空間です。
無限次元空間と言われると、馴染みのない人は半分冗談でしょという顔をするのですが、実は高校生でも内容に触れているのです。
余談ですが、命題に述べた三角関数の性質は、フーリエ級数展開に関係があります。大学 2・3 年生でより詳しく勉強することになるでしょう。その際はオイラーの公式 \(e^{i n x} = \cos nx + i \sin nx\) を踏まえて、指数関数の集合 \(\{ e^{i n x} / \sqrt{2\pi} \} _ {n = -\infty} ^ \infty\) を考察することになります。
変分法について
汎関数
さて、話戻しましょう。
関数 \(f\) の定義域を、ユークリッド空間から関数空間 \(H\) にしようという話でした。この変更をすると、考えている \(f\) は「関数空間 \(H\) を定義域として、実数値を返す関数」になります。これを汎関数と言います。
そして、変分法とは、汎関数の臨界点を調べる一連の手法のことです。
汎関数は普通 \(I\) という記号をおきますので、以下ではこれを用います。つまり \( I \) は関数空間 \( H \) を定義域として、実数を返す関数です。このことを \(I \colon H \to \mathbb{R}\) と表記します。ここで、実数全体の集合を \(\mathbb{R}\) と書きました。高校までの教科書では使われない記号ですが、大学に入るとよく使う記号です。
汎関数の微分
定義域をうまく設定すると、汎関数 \(I\) の微分を考えることができます。ガトー微分、フレッシェ微分などと呼ばれるものです。フレッシェ微分した後の \(I’\) は、 \(u \in H\) を定めるごとに汎関数になります。
(この段落はわからなければ飛ばして良いです) つまり \(I'(u) \colon H \to \mathbb{R}\) となります。換言すれば \(u, v \in H\) に対し \(\langle I'(u), v \rangle\) は実数です。プログラミング言語に強い人は高階関数をご存知でしょう。 \(I\) は汎関数、つまりプログラミング言語でいうところの \(1\) 階の高階関数です。 \(I’\) は、関数を引数にとり、汎関数を返します。つまりプログラミング言語でいうところの \(2\) 階の高階関数です。
微分方程式に変分法が有効な理由
さて、変分法の話をしばらくしてきましたが、元はといえば微分方程式の話でした。 \(I’\) がどうして微分方程式と関係するのでしょうか。
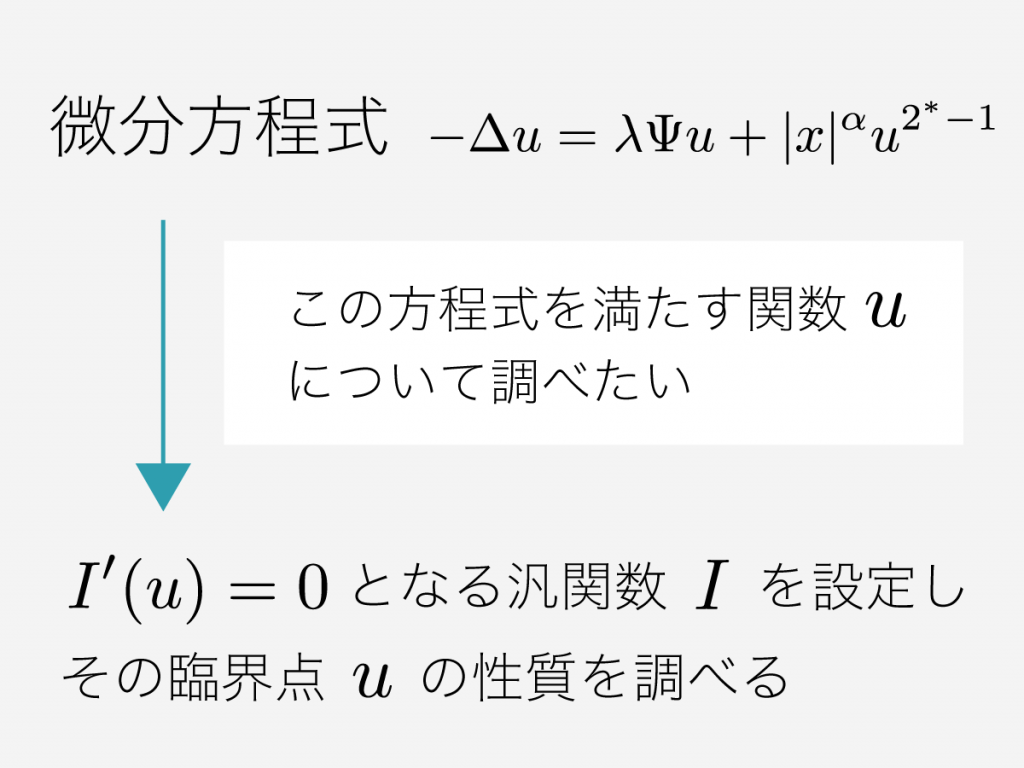
実は \(I\) の臨界点、すなわち \(I'(u) = 0\) となるような関数 \(u\) が、自分が考察したい方程式の解となるように、 \(I\) を設定することができます。
少々の誤解を恐れずに言えば「 \(I'(u) = 0\) 」が「元の方程式」となるように、 \(I\) を設定します。
そして方程式を直接調べる代わりに、 \(I\) の臨界点 \(u\) の性質を調べます。これが変分法の基本的な考え方です。
例えば \(I\) の臨界点 \(u\) の存在を示せば、解の存在を示せます。先人たちの知恵が整っているので、 \(u\) の境界条件・初期条件や解の滑らかさ、解が正値であるかどうかといった解の性質も、色々な知見を組み合わせてわかります。
ですから、変分法は微分方程式を考察するためには、強力な手法です。変分法と微分方程式が、ここで繋がるわけです。
補足
念の為に補足しておきますが、全ての微分方程式が変分法で考察できるわけではありません。万能というわけではありません。変分法以外にも、微分方程式を考察するために、人類は様々な手法を開発してきました。
対象とする微分方程式の特性に応じて、有効な手法は様々です。そのような手法の種類が非常にたくさんあって、いわば未開のジャングルを探索している状態になっていることが、微分方程式という数学の分野の重要な特徴だと私は思います。
ただし、偏微分方程式を考察するための最も基本的で重要な手法が変分法であることは、多くの専門家がそう認識していると思います。いわば変分法は偏微分方程式の王道です。過去も、現在も、そうあり続けています。そして近い未来までは、きっとそうだと思います。
他分野との変分法の捉え方の違い
現在の日本の標準的な理系の大学のカリキュラムですと、大学入学後、初めて変分法を習うのは、数学ではなくて物理学である可能性が高いと思います。
私見では、数学と他分野では、変分法の「捉え方」がだいぶ違います。その違いについて述べます。
高校生の物理では、光学でフェルマーの原理を習います。「物質を透過する際に、光はその光学的距離が最小となるような経路をとる」という内容です。
実は、光学に限らず、物理学では「実際に起こる『現象』は『何か』が最小となるものである」という特徴付けが、非常に多くの場面でなされます。「最小作用の原理」と呼ばれます。最小作用の原理は、物理学の基本原理であるとも言われています。
具体例として、少し進んだ例を出します。高校生で習う古典力学は、大学 1 年生でも見直すことになりますが、大学 2 年生でさらに高度な捉え方をすることになります。これを解析力学と呼びます。
解析力学で取り扱われる最初の話は、「実際に起こる『運動』は『ラグランジアン』が最小となるものである」というものです。そしてこの『ラグランジアン』 \( L \) は、汎関数(関数空間を定義域とする関数)なのです。
そしてその話の直後に、 \( L \) を最小化する関数 \( u \) が充たす微分方程式として、オイラー・ラグランジュ方程式を導きます。その解 \( u \) が実際の『運動』です。そしてオイラー・ラグランジュ方程式を深く考察して、解析力学の前半部分が終了します。
さて、この解析力学の話と、上で述べた微分方程式の数学的研究の話を比較しましょう。するとこの両者は、ちょうど順番が逆の議論をやっていることになることがわかります。
つまり『ラグランジアン』 \(L\) は汎関数で、『運動』 \(u\) は関数空間の臨界点です。解析力学では \(L\) の臨界点 \( u \)が充たす方程式としてオイラー・ラグランジュ方程式を「導き」、オイラー・ラグランジュ方程式を考察するという順序になっています。
しかし、変分法の数学的研究では、考察したい微分方程式がまずあって、その解を考察することがまず動機になります。そこで、臨界点が方程式の解となるように汎関数 \(I\) を「設定」して、 \( I \) の臨界点を考察する、という順番になっています。
どちらも「変分法」「変分原理」と呼ばれます。何れにしても「汎関数の臨界点は、対応する微分方程式の解になっている」という事実が鍵となっています。

数学の間でも変分法の捉え方の違いがある
ついでにいうと、最先端の変分法の研究は、上で述べた問題意識とは異なることもあります。一言だけ述べておきたいと思います。
今まで私は、変分法とは微分方程式の研究をするための手法だと述べてきました。「 \( I'(u) = 0 \) 」が「考察したい微分方程式」となるよう、対応する汎関数 \( I \) を「設定」すると述べました。
ところが、現代の変分法の研究では、まず \( I \) の方を適当に設定して、 \( I \) の臨界点を考察することそのものが動機になる場合もよくあります。
これは面白い動機の変化です。この場合も、 \( I \) に対応する微分方程式「 \( I'(u) = 0 \) 」を調べていること自体は、間違いないことです。しかし、それは結果論で、むしろ変分法そのもの、つまり汎関数 \( I \) の臨界点を見出すことそのものに興味がある数学者も多くいます。
このことを指してしばしば「変分法の研究では、微分方程式はおもちゃ」と呼ばれることもあります(私はそうは考えてはいませんが…)。
臨界点の求め方
微分が \(0\) になる点を臨界点と呼びました。変分法とは、汎関数の臨界点を求めることだと述べました。そこで、臨界点を求める方法について話したいと思います。
高校の数学 III でも臨界点を求めますが、これは定義域が実数のある区間、要するに \(1\) 次元でした。大学 \(1\) 年生では定義域が \(2\) 次元の場合を中心に、 \(N\) 次元空間での臨界点を調べる方法を学びます。
ところが、今取り扱っている汎関数 \(I\) の定義域 \(H\) は無限次元空間です。 無限次元空間で臨界点を求めるのは、有限次元の場合と難易度が全く異なることです。臨界点の存在が示されるだけでも高度なことだと言えます。そこで、臨界点の存在を示す代表的な方法の概要を紹介します。
極小点を求める方法
1 つは、 \(I\) の極小点を求めるという方法です。
滑らかな関数であれば、極小点において微分は \(0\) になります。このことは無限次元でもさほど事情は変わりません。これは変分法の原始的で基本的な考え方です。
つまり高校や大学 1 年生までと、ものを考える順番が逆になっているのです。高校や大学 1 年生までは、極小点を求めるために関数を微分し、臨界点をまず確定させました。変分法の場合は、臨界点の存在を示すために、極小点を求めにいきます。
例えば、極小点に近づく点列をまず得て、その極限が存在すること、およびその極限が極小点に実際になっていることを示します。これで臨界点を求めたことになります。
「馬の鞍の点」を求める方法
ところが、もう一つ、上記とは異なる、重要な考え方があります。そう、最初の話を思い出して欲しいです。
臨界点は、必ずしも極小点・極大点にはなりませんでした。 \(2\) 次元空間では、馬の鞍の形をした臨界点もありうると。
あの形の臨界点を求めることも、現代の変分法の研究においては重要な課題です。
\(2\) 次元空間の馬の鞍の形の場合、臨界点の周りは \(1\) 次元方向では上がっていて、もう \(1\) 次元方向では下がっていました。
無限次元空間でも「ある \(d\) 次元方向では下がっていて、残りの方向では上がっている」という点を、しばしば、捕まえることができます。こちらの研究が、近年では主流になっています。
私は \(d = 1\) の解について調べるのが、主な専門となっています。その具体的な手法や定理については…ここから先を述べるのはとても高度なので、ここで筆を置かせていただきます。
終わりに
まとめ
ここまで述べた内容をまとめておきます。
- 無限次元空間は、存在します。高校生でも、具体例に触れています。
- 変分法とは、無限次元空間で臨界点を探す一連の手法を指します。
- 汎関数の臨界点は、対応する微分方程式の解になっています。これを利用して今も微分方程式の最先端の研究が行われています。
以上の内容に興味がある方は、数学科に来て修士課程 1 年生まで勉強すると、正確にわかるようになります。
そうでなくても、理系の学部に来ると、大抵、なんらかの形で、上で述べたことに関連した話題に触れると思います。その時、「あの時読んだことは、こういうことだったんだ」と、この記事を読んだ体験を思い出していただければ、私は嬉しいです。
読書案内、参考文献
参考文献を挙げます。といっても、微分方程式や変分法の数学的研究をするには、大学入学後数学を 4, 5 年程度勉強する必要があります。そこで、段階に応じた読書案内をしたいと思います。以下では数学科の標準的なカリキュラムを参考に「\( n \) 年生向け」のように書きますが、自分の数学力が足りていれば自分の学年より上の文献にも手が届くでしょう。
大学 1 年生向け
上の話で多変数関数の極大点、極小点について書きましたが、まずこの話については微分積分の教科書に書いています。例えば
- 牛腸徹『数学IB演習プリント』
がわかりやすいでしょう。その上でより定式化された微分積分を読むとなおよろしいでしょう。
- 杉浦光夫『解析入門 I』『解析入門 II』
は、牛腸先生のプリントに続けて読むのにはちょうどよく、記述が丁寧です。あとルベーグ積分について少しお話ししましたが、これについては
- 新井仁之『ルベーグ積分講義―ルベーグ積分と面積0の不思議な図形たち』
の前半は 1 年生向けに書かれています。
大学 3 年生向け
数学専攻の大学 3 年生だと、何らかの方法でルベーグ積分までは勉強することになると思います。関数空間・フーリエ解析について本文中に述べましたが、それらを続けて勉強するのが大事です。例えば以下の本が私は好きです。
- エリアス・M・スタイン、ラミ・シャカルチ『実解析 (プリンストン解析学講義 III)』
- 吉田伸生『ルベーグ積分入門―使うための理論と演習』
- 新井仁之『新・フーリエ解析と関数解析学』
- 黒田成俊『関数解析』
- 宮寺功『関数解析』
- W. Rudin “Real and Complex Analysis (Third Edition)”
大学 4 年生向け
微分方程式については、例えば、
- Lawrence C. Evans “Partial Differential Equations (Second Edition)”
に、微分方程式で使われる様々な手法のエッセンスが載っています。色々な手法をみた後に、変分法を専門にしようと考えるならば、
- 田中和永『変分問題入門』
をまず読んで、その参考文献に書いてある詳しい教科書を当たると良いでしょう。
その他
冒頭に掲げた積分方程式の問題の出典は、 2019 年度の早稲田大学商学部の数学の入試問題です。
途中の図で出てきた微分方程式は、以下の論文から採りました。
- Kazune Takahashi “Positive solution for an Hénon type equation with critical Sobolev growth”, Electronic Journal of Differential Equations 2018(194) (2018) 1-17.
謝辞
この記事を執筆する際、草稿段階から Laborify 代表の青松さんからたくさんの有益なコメントをいただき、更に綺麗な図を作っていただきました。青松さんのご指摘は具体的で、記事をよくするための書き直しもしやすかったです。変分法は高度な内容ですが、最終的にできたこの記事がわかりやすいと思っていただけたならば、青松さんのおかげです。本当にありがとうございました。