はじめまして.名古屋大学大学院 多元数理科学研究科 修士2年の齋藤耕太と申します.大学院では微細な構造を持つ図形について扱うフラクタル幾何学と整数の性質について扱う整数論について主に研究しております.
修士の2年間は特にフラクタル次元と呼ばれる尺度と等差数列との関係について研究してきました.この記事を通じて等差数列のおもしろさを少しでも解っていただけたらと思います.
目次
ボードゲームから始める等差数列
APG (等差数列ゲーム)
まず,数学的な話をする前に私が大学4年のときに研究室の友人たちと作ったボードゲームAPGについて紹介します.APGとは
Arithmetic Progressions’ Game
の略で,四目並べの拡張です.日本語で言うと「等差数列ゲーム」といいます.主なルールは以下の通りです:
- 3人以上の多人数で行う.自分のターンが回ってきたら1人1つ駒を置く.
- 一直線上等間隔に4個以上並べたプレイヤーの勝利.横の図だと桂馬の動きでもよい.また赤の×の間に他の駒があっても赤の勝利.
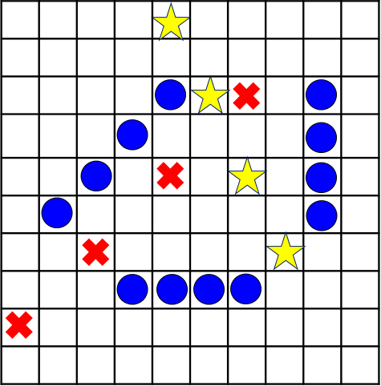
- リーチの状態になったとき「APG」と宣言しなければならない.
実際にゲームをプレイしたほうがいいですが,ここでは例を挙げます.
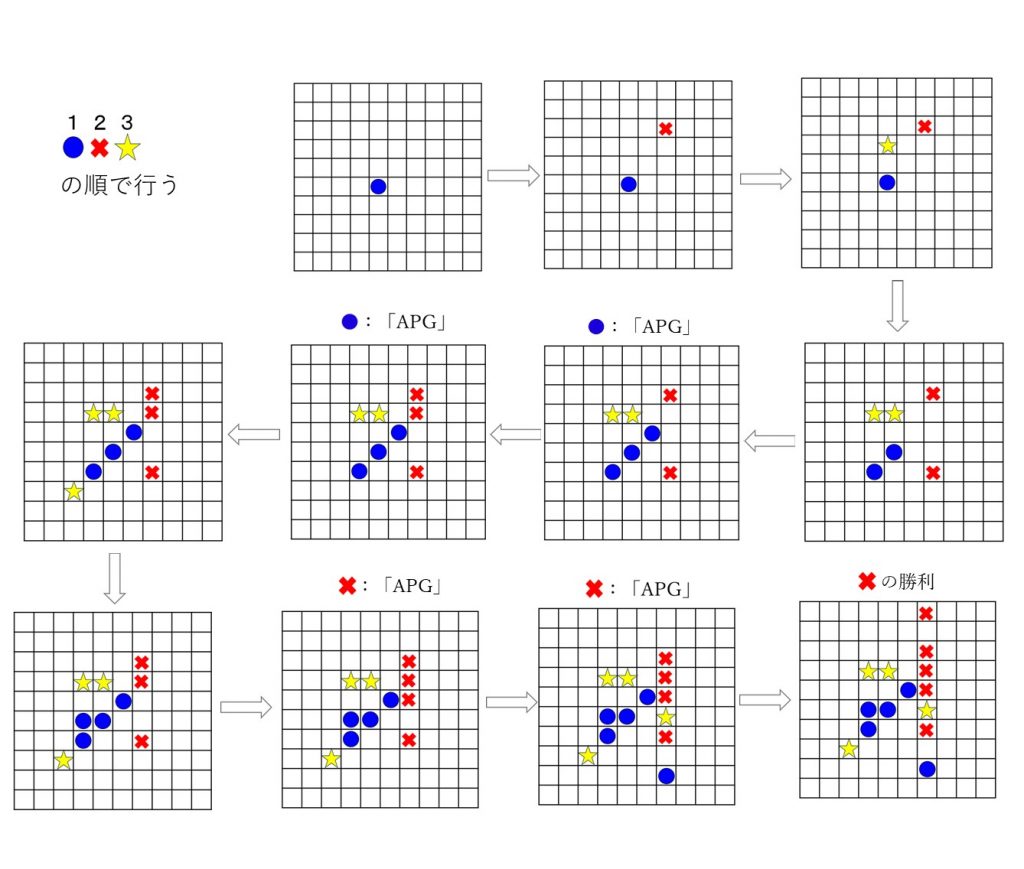
ではここで,次の問題を考えましょう.
問題A: 十分大きいゲームボードを使って3人でAPGを行ったとき,引き分けは起こりうるか?
すなわち「 十分大きいゲームボードを用意したとき, 3人とも自分の駒が一直線上等間隔に3個以下しか並んでなく,かつゲームボードをコマで全ていっぱいにすることができるのか?」という問題です.引き分けのイメージ図は以下となります.ただし,これはあくまでイメージ図で探してみると一直線上等間隔に4個ならんでいる駒があり,引き分けにはなっていないです.

ファン・デル・ヴェルデンの定理
問題(A)の答えは
十分大きいゲームボードを使い3人でAPGを行うと,引き分けは起こらない
ということがファン・デル・ヴェルデンの定理という定理を使うと保証されます.ファン・デル・ヴェルデンの定理とはファン・デル・ヴェルデンが1927年に証明した定理です.どのような定理かAPGの言葉を使って説明しましょう.
まず,\(~r~\) 人で\(~k~\) 個等間隔に並べれば勝利するAPGを次の帯で行います.帯の場合も平面と同じで,ゲームは成立します.自分のターンが回ってきたら1人1つ駒を置き,等間隔に\(~k~\)個並べれば勝ちです.

このとき,帯の長さ \(~n~\) を十分大きくすると,必ず誰かしらは勝利する.という定理です.つまり,人数と勝利条件に応じて十分長い帯でAPGを行うと,必ず誰かしらの駒は等間隔に\(~k~\)個並ぶという定理です.これは「帯」という1次元のものですが,「平面」で考えても同様のことが起き,人数と勝利条件に応じて十分大きいゲームボードを用意すれば必ず誰かしらは勝利するということがわかります.では,
十分大きいとはどのくらいなのか?
ということが次に気になるところです.いまのところ, 3人で一直線上等間隔に4個並べれば勝利するAPGを行うとき,(縦×横=)293×293の以上のサイズのゲームボードを用意すれば必ず誰かしらは勝ちます.しかし,このサイズが最小であるのかはわかっていません.
以上の議論から次がわかりました.
問題: 十分大きいゲームボードを使って3人でAPGを行ったとき,引き分けは起こりうるか?
解答: 293×293以上のサイズのゲームボードを使えば,必ず誰かしらは勝利する.しかし,必ず誰かしらは勝利するようなゲームボードのサイズの中でこのサイズが最小であるかはわかっていない.
最小のサイズを求めるような研究もありますが,簡単そうに見えて一般にはとても難しいです.例えば,\(~r~\) 人で一直線上等間隔に\(~k~\) 個 並べれば勝利する1次元のAPGについて言及すると,帯の長さを
\[2^{2^{r^{2^{2^{k+9}}}}}\]
以上にすれば誰かしらは勝利します.これは,数学のノーベル賞といわれているフィールズ賞を受賞した数学者ガワーズの結果を用いるとわかります.
この数は凄まじく大きいです.例えば\(~r=5~\), \(~k=4~\)を代入してみると,
\[2^{2^{5^{2^{2^{13}}}}}\]
となります.正直大きすぎてイメージし辛いです.この数を通常の10進法で書き下して,A4用紙1枚につき1500文字を印刷し,その紙を積み重ねていくとしましょう.ただし,A4用紙100枚の厚さを1cmとします.紙のタワーができるわけですが,どのくらいの高さになるでしょうか?
答えは,私たちが観測できる宇宙の直径よりもはるかに大きい!!
本当に大きすぎるので改善したいです.
※私は天文学や宇宙物理学はわからないので,JAXAのサイトから「観測できる宇宙の大きさ」を参考にし,宇宙が137億年前に誕生したものとして,137憶光年を観測できる宇宙の大きさとしました.参考文献に載せておきます.
等差数列の包含問題
一直線上等間隔の点列について述べていきましたが,ここでこの列に等差数列という名前を付けましょう.より明確にいうと,「一直線上等間隔に\(~k~\)個並んだ点列のことを項数\(~k~\)の等差数列」というようにします.

これまででどのような問題が考えられてきたかというと,
与えられた数列にどのくらい項数の大きい等差数列が存在するか?
という問題がよく研究されてきました.この問題を等差数列の包含問題と言います.悲しいことに日本での研究者はとても少ない分野でもあります.
この問題について具体例をあげて説明しましょう.例えば,素数からなる等差数列について考えましょう.素数とは自分自身と1のみでしか割れない2以上の整数のことを言います.
\[2,\ 3,\ 5,\ 7,\ 11,\ 13,\ 17,\ 19,\ 23,\ 29,\ 31,\ 37,\ 41,\ 43,\ 47,\ 53,\ 59, \cdots \]
が素数の例として挙げられます.ここで,素数からなる項数3の等差数列を探してみると,\[ \{3,\ 5,\ 7\},\quad \{31,\ 37,\ 43\}\] など見つけることができます.では,素数からなる項数4の等差数列は存在するでしょうか? 探してみると\[\{41,\ 47,\ 53,\ 59\}\]などが見つかります.項数5についてはどうでしょうか? これも\[ \{5,\ 11,\ 17,\ 23,\ 29\}\]という数列が見つかります.そこで,
素数はどのくらい項数の大きい等差数列を含むか?
この問題はグリーンとタオによって2008年に解決され,「どこまでも大きくできる」ということが証明されました.すなわち,項数100であろうが1000であろうが10000であろうが,その項数の素数からなる等差数列が存在するのです.ただし,具体的にその等差数列が何なのかわかっているわけではなく,少なくとも「存在すること」のみが保証されています.
数学ではこのようなことがしばしば起こります.例えば,パーティーの会場に367人いるとしたら必ず誕生日が同じ2人組を見つけることができます.具体的にどのペアが誕生日が同じなのかはわかりませんが,そのようなペアが「存在すること」のみが保証されるのです.
サイズが大きければパターンが存在する.
前に数学的には十分サイズの大きいゲームボードを用意すれば必ず誰かしらのコマは一直線上等間隔に4個ならんでしまうことを述べました.このように,サイズが大きければ,パターンが存在するということは数学ではよくあります.
グリーンとタオもセメレディの定理と呼ばれる定理を拡張して,それを素数に適応させるという証明方法を用いて素数からなるいくらでも大きい項数の等差数列の存在を示しています.セメレディの定理については詳しくは述べませんが,これも「サイズ」が大きければいくらでも大きい項数の等差数列が存在するといった主張です.詳しくは参考文献をご覧ください.
上記の議論は整数についてのことですが,実数の世界でも同じように「サイズ」を測ることで等間隔の点といった「パターン」を導出することができないのでしょうか? それがこの記事で紹介する私の研究です.より具体的にいうと,
フラクタル次元が十分に大きい図形は等間隔の点をもつか?
という問題を研究しています.フラクタル次元については次に記します.
図形の「粗さ」を測るフラクタル次元
フラクタルとは?
フラクタルとは図形の全体が一部と何らかの意味で「似ている」細かい構造をもった図形のことを指しますが,数式を使って定義するのが非常に難しい言葉です.フラクタル幾何学を創ったマンデルブローは「フラクタル」に数学的に厳密な定義を与えたものの,その定義から興味深い図形を除外してしまっているという欠陥もありました.未だに誰もが認める「フラクタル」の数学的な定義はないと思います.またその定義の難しさについてフラクタル幾何学の専門家であるファルコナーは自身の著でこう記しました:
私の個人的な感覚では,「フラクタル」の定義は,生物学者にとっての「生命」の定義と同じように考えるべきものである.
K. Falconer (著),服部久美子,村井浄信 (訳) 『新しい解析学の流れ フラクタル幾何学』,共立出版,2006,pp. xxvi.
私はこの文言が好きです.個人的には,厳密さを求める数学で研究対象の「フラクタル」という言葉が数学的に未定義という点はおもしろいところでもあると思います.フラクタル幾何学は不規則すぎる図形や「病的」とされた例外的な図形を扱う幾何学なので,無理に分類分けするよりこのくらい緩やかなのが丁度よいのかもしれません.
ちなみに,「フラクタル」という言葉を最初に提唱したのはマンデルブローで「壊れている」という意味のfractusから取ったとされています.数学的でなくても言葉の定義はする必要はあるので,ここでは「フラクタル」といったら図形の全体が一部と何らかの意味で「似ている」細かい構造をもった図形を指すこととします.
では,典型的なフラクタルの例である自己相似図形について説明しましょう.自分自身と相似な図形で構成された図形のことを自己相似図形といいます.
例えば,次の図形はシェルピンスキー・ガスケットと呼ばれている自己相似図形です:

この図形は正三角形を四つの合同な正三角形に分割して,真ん中を取り除くという操作を無限回繰り返すとできる図形です.おもしろいことにシェルピンスキー・ガスケットの面積は0になります.面積が0になる図形の例として,例えば線分が挙げられるので,面積で見るとシェルピンスキー・ガスケットは線分に近い性質を持つことが予想できます.
一方,長さはどうなるのでしょうか? 線分に似た性質を持っていれば シェルピンスキー・ガスケットの長さは有限の値をとってほしいものです.しかし,計算してみるとシェルピンスキー・ガスケットの長さは無限大になります. 長さが無限大になる図形の例として,例えば面が挙げられます.よって,長さという観点からはシェルピンスキー・ガスケットが面に近い性質を持つことが予想できます.
ここで,次の問題を考えましょう:
シェルピンスキー・ガスケットは 何次元の図形なのか?
長さが無限大で面積が0の図形です.すなわち,1次元と2次元の間の性質をもつということですが,このような中間体の「形」を扱えるのがフラクタル幾何学のよいところです.
フラクタル次元とは?
そもそも物や図形の「次元」とは何なのでしょうか? これを数式を使って定義するのは困難でしょう.この記事では私が扱っているフラクタル次元について解説しますが,フラクタル次元も誰もが納得するような数学的に厳密な定義はないと思います.これもフラクタル幾何学のおもしろい点ですが,研究対象の「フラクタル」も数学的には未定義で上に,主な道具の「フラクタル次元」も数学的に未定義なのです.
ただし,これは数学的な議論ではなく私の偏見が入っているので,他の研究者と意見を共有しないこともしばしばあります.ご了承ください.
ではここで,フラクタル次元とは何なのでしょうか?
フラクタル次元とは2つの意味で使われます.1つはハウスドルフ次元やパッキング次元,アッパーボックス次元など図形の「粗さ」を測る尺度の総称です.2つ目はハウスドルフ次元やパッキング次元,アッパーボックス次元など,特定の次元を指してフラクタル次元と呼んだりします.
これらハウスドルフ次元やパッキング次元,アッパーボックス次元は数学的に厳密に定義されています.単にフラクタル次元という言葉を使用するときは注意が必要で,書き手が総称として用いているのか,もしくは特定の次元を指して使用しているのか気にする必要があります.
この記事ではアッパーボックス次元と呼ばれる次元を採用することとしましょう.様々な同値な定義がありますが,アッパーボックス次元とは図形の「粗さ」を正方形を数えることで測る尺度です.ここでは厳密な定義は与えずに簡単な解説をします.
平面内の図形を\(~F~\)とします.正の実数\(~r~\)に対して,\(~N(F,r)~\)を図形\(~F~\)を覆うことのできる一辺が\(~r~\)の正方形の最小個数と定義します.このとき,上極限\[\limsup_{r\rightarrow +0} \frac{\log_{10} N(F,r)}{\log_{10} (1/r)}\] を図形\(~F~\)のアッパーボックス次元といいます.
ここで上極限\(\limsup \)については説明を省きますが,極限と同じようなものです.振動する関数や数列に対して極限は定義できませんが,上極限はそのように振動するものに対しても定義できます.よって,ここでは極限が存在するか否かを気にする必要はないです.
とにもかくにも重要なのはシェルピンスキー・ガスケットのような自己相似図形だけではなく,
どんな図形に対してもアッパーボックス次元を定めることができる
ということです.
※対数関数の底は正の実数であればなんでもよいです.というのも,底をどのような数でとっても底の変換公式によりアッパーボックス次元は不変ということがわかるからです.今回は対数関数\(~\log~\)の底を10として常用対数を用いましたが,通常は自然対数を用います.
具体的にどう測るの?
ここで,具体例を計算してみましょう.図形\(~F~\)を次の曲線とします.ただし,縦横の比を変更してもアッパーボックス次元は不変なので適当に比を変えたものを挙げています:
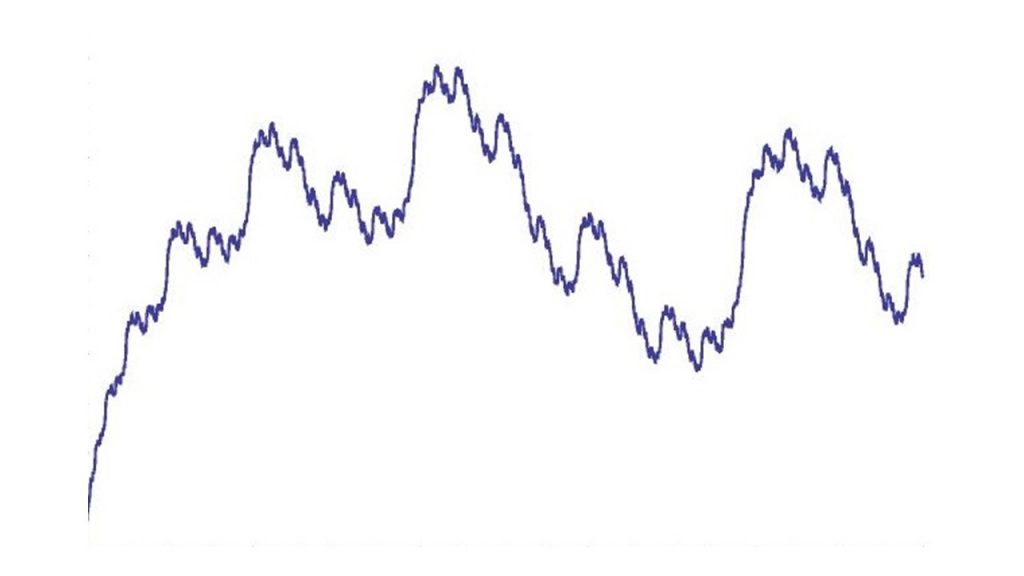
Wolfram|Alpha を用いて書いた.
次に,\(N(F,0.1)\)を求めてみましょう.一辺が0.1の正方形で曲線\(~F~\)覆ったものが次のようになります:
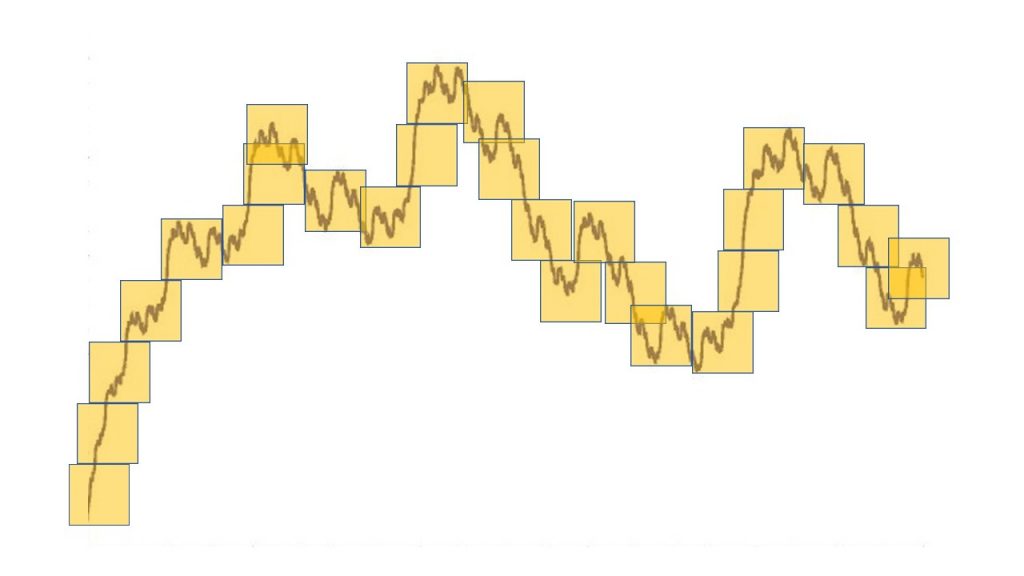
図のように27個の正方形で覆うことができました.\(~N(F,0.1)~\)の定義を思い出すと,図形\(~F~\)を覆うことのできる一辺が\(~0.1~\)の正方形の最小個数でした.よって,\[N(F, 0.1)\leq 27\] ということがわかります.ここでは簡単のため, \(N(F, 0.1) = 27\)として計算します.すると,\[
\frac{\log_{10} N(F,0.1)}{\log_{10} (1/0.1)} = \frac{1.431}{1} =1.431 \]がわかりました.
次に0.1よりもさらに小さい正の実数で同様のことをします.ここでは0.05として計算しましょう.すなわち,\(N(F,0.05)\)を求めます.一辺が0.05の正方形で曲線\(~F~\)覆ったものが次のようになります:

図のように69個の正方形で覆うことができました.\(~N(F,0.05)~\)の定義を思い出すと,\[N(F, 0.05)\leq 69\] ということがわかりますが,同様にして, \(N(F, 0.05) = 69\)として計算します.すると,\[
\frac{\log_{10} N(F,0.05)}{\log_{10} (1/0.05)} = \frac{1.839}{1.699} =1.082 \]ということがわかりました.
同様の操作を繰り返して,正方形の1辺をどんどん小さくしていき,\[ \frac{\log_{10} N(F,r)}{\log_{10} (1/r)}\]が「近づいていく値」を\(F\)のアッパーボックス次元と呼びます.ここで,かっこ付きで「近づいていく値」と書いた理由は,上極限を厳密には取らないといけないので,どう近づいていく値を上極限と呼ぶのか議論する必要があるからです.ここでは省略します.
ちなみに,曲線\(F\)のアッパーボックス次元の理論値は1.2次元となります.アッパーボックス次元が整数になるときもありますが,非整数次元となることもあるのです.
シェルピンスキー・ガスケットの次元
シェルピンスキー・ガスケットのアッパーボックス次元を測りましょう.一辺が\(~r=1/2~\)の正方形でシェルピンスキー・ガスケットを覆います.簡単のため,ここでは正方形を整列させて覆っています.
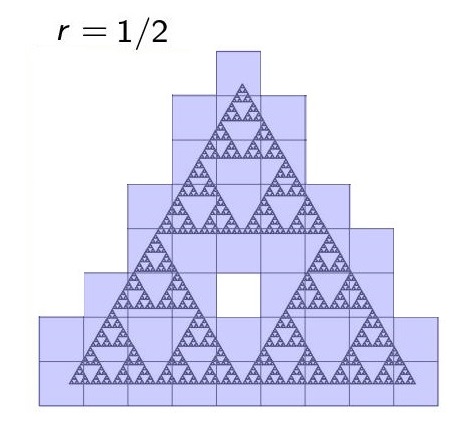
正方形は42個必要でした.さらに,小さい正方形で次の図のように覆っていきます:
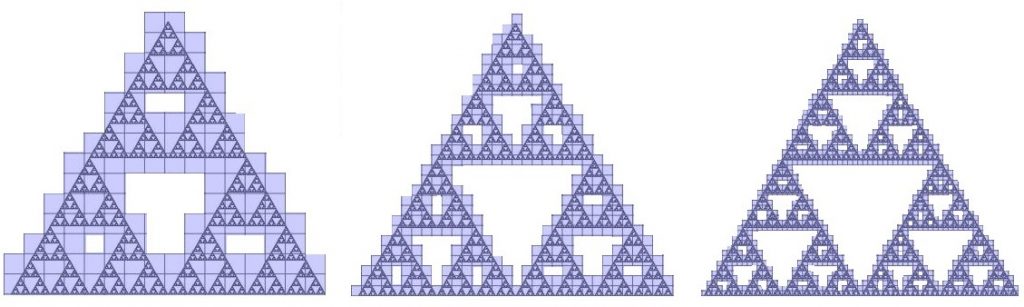
正方形の個数と正方形の一辺の長さとの関係をみることで, \[\limsup_{r\rightarrow +0} \frac{\log_{10} N(F,r)}{\log_{10} (1/r)}\] の実験値を計算してみると,
1.512次元
となりました.ちなみに,理論値は
\(~\log_2 3~\) (=1.584…) 次元
となります.シェルピンスキー・ガスケットは長さが無限大で面積が0の図形でした.そのような線でも面でもない感覚的には中間の図形の次元を明確に実数値で表してくれるところがアッパーボックス次元のよいところです
アッパーボックス次元の意味
次にこの次元にどのような意味があるのか他の例を挙げて説明しましょう.
平面内に描かれた図形についてはアッパーボックス次元が1に近ければ近いほど,その図形は滑らかな線に近づき, そして,アッパーボックス次元が2に近ければ近いほど平面的な広がりをもつ図形に近づいていきます. 例えば,次のようになります:
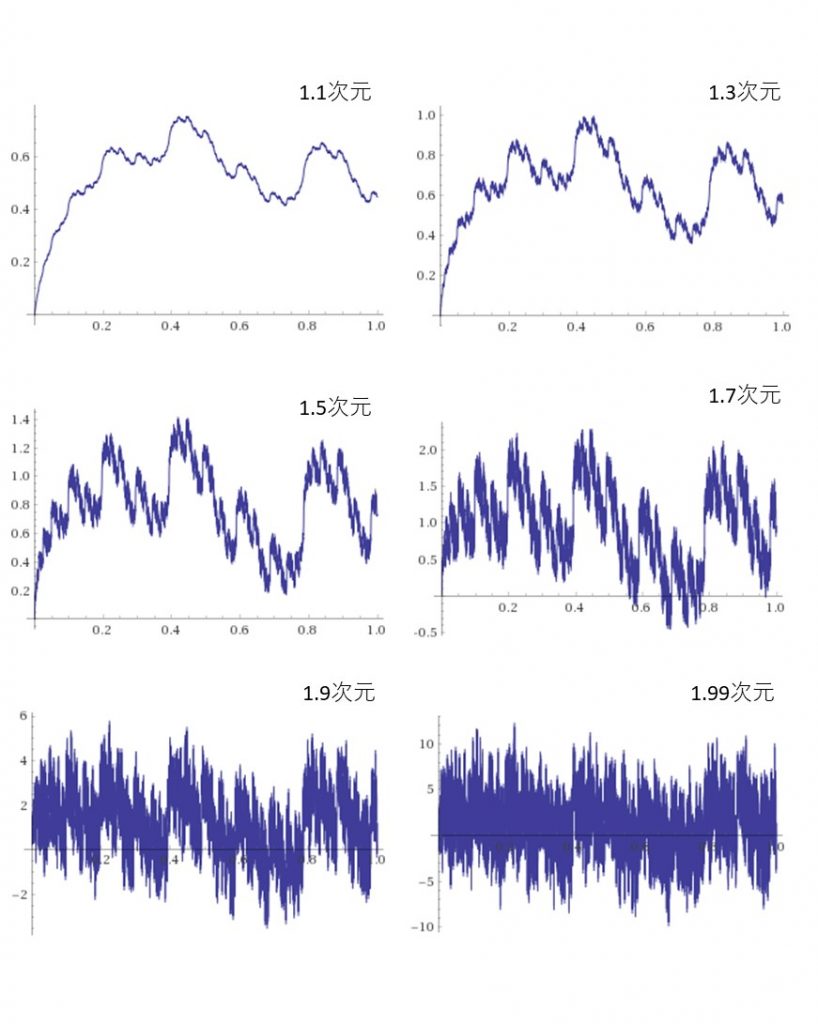
ちなみにこれらの曲線を定める関数は\(~1<s<2~\)なるパラメータ\(~s~\)を用いて全て
\[ y=\sum_{k=1}^\infty 2^{(s-2)k} \sin (2^k x),\quad (0\leq x\leq 1) \]
と書けます.
上のグラフから,アッパーボックス次元が2に近ければ近いほど,図形が平面的な広がりを見せていくということがわかります.ではここで,本題の等差数列に戻りましょう.
ケレティの反例
サイズが大きければパターンが存在してしまうということをボードゲームAPGを用いて説明しました.そのことを念頭に置いて次の問題を考えます:
アッパーボックス次元が2である図形は
いくらでも大きい項数の等差数列を含むか?
ここで等差数列について一度復習しましょう. 「一直線上等間隔に\(~k~\)個並んだ点列のことを項数\(~k~\)の等差数列」と言いました.
平面はいくらでも大きい項数の等差数列を含みます.また,アッパーボックス次元が2である図形は平面的な広がりを「ほぼ」もつので,いくらでも項数の大きい等差数列を含みそうです.しかし,1998年に証明されたケレティの結果から
アッパーボックス次元が2であり,
項数3の等差数列を含まないような図形が存在する.
ということがわかるのです.ここで1つ注意ですが,項数3の等差数列を含まないような図形は項数4,5,6,…の等差数列も含みません.
項数3の等差数列を含まないような図形は直観的にはボロボロに壊れた図形になるはずですが,そういった図形でアッパーボックス次元が2になるものを構成することができるとは正直驚きです.
少し注意ですが,ケレティが証明した結果はもっと強いことを言っているので気になる方は下の参考文献から原論文を見てください.
自身の研究
弱い等差数列
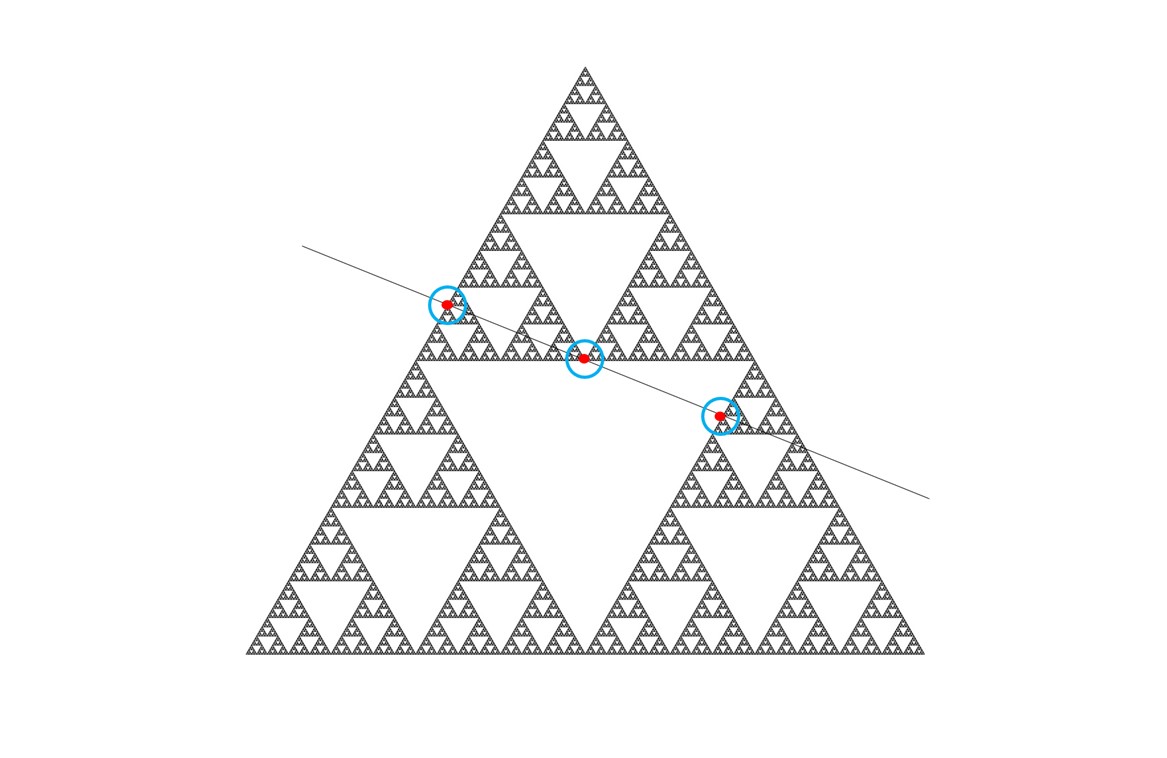
ケレティの結果によりサイズ(次元)が大きくても,(項数3の)等差数列があるとは限らないということが導かれてしまいました.感覚的にはおかしな定理です.そこで,私はフレイザーとユーというスコットランドの研究者との共同研究で弱い等差数列を考えました.ここでいう「弱い等差数列」とは下の図の赤い点列のように等差数列の近くにある「おおよそ」等間隔の点という意味です.
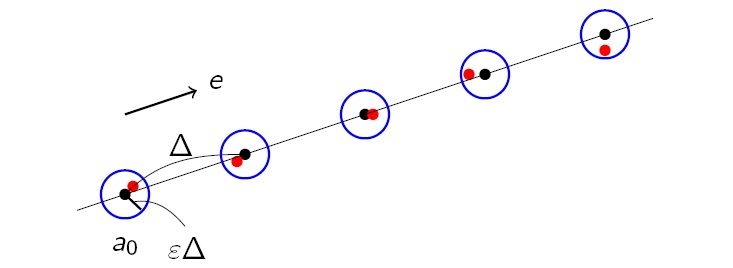
そこで考えた問題が
アッパーボックス次元が2に十分近い図形は
どのくらい大きい項数の弱い等差数列を含むか?
という問題です.
研究結果
フレイザーと私とユーによる共同研究で
各3以上の自然数\(~k~\)に対して,アッパーボックス次元が\(~k~\)に応じて十分2に近い図形は項数\(~k~\)の弱い等差数列を含む.
ということがわかりました.APGでは,十分大きいサイズの大きいゲームボードを用いると必ず誰かしらは一直線上等間隔の列ができました.
実数の場合についてはサイズとしてフラクタル次元を用いると,ケレティの結果から真の等間隔の列の存在は保証できませんが,フラクタル次元が十分に大きいとき,「おおよそ」等間隔に並んだ列なら存在するということが明らかになりました.
※ 厳密にはアッパーボックス次元ではなくアソード次元というフラクタル次元を用いていたり,弱い等差数列の弱さを示すパラメータとして \(\epsilon\) というものを用いていたりしますが,大部分を省略しました.
終わりに
まとめ
長々と書きましたがまとめると以下となります.
- 一直線上等間隔に4つ並べたプレイヤーが勝利するゲームをAPGといった.
- 十分大きいゲームボードでは必ず誰かしらは勝利する.
- サイズが大きければ,パターンができる.
- 実数に置き換えると,フラクタル次元が十分大きければ,弱い等差数列が存在するという結果を得た.
今後はフラクタル次元を用いた弱い等差数列の存在定理が整数の等差数列の存在定理に及ぼす影響について研究したいと思います.
以上のことで質問やご意見等ありましたら,私のメールアドレス
m17013b@math.nagoya-u.ac.jp
までよろしくお願い申し上げます.
参考文献
ファン・デル・ヴェルデンの定理について,原論文は
- B.L. van der Waerden, Beweis einer Baudetschen Vermutung, Nieuw. Arch. Wisk., 15 (1927), 212–216.
が挙げられますがドイツ語なので,日本語だと
- ア・ヤ・ヒンチン (著), 蟹江 幸博 (訳), 『数論の3つの真珠 (はじめよう数学)』,日本評論社,2000.
- INTEGERS 『ファン・デル・ヴェルデンの定理』 http://integers.hatenablog.com/entry/2017/03/08/025731
が詳しいと思います.ガワーズの上界について,原論文は
- W.T. Gowers, A new proof of Szemerédi’s theorem, Geom. Funct. Anal., 11 (2001), 465‐588.
です.日本語の解説は発見できませんでした.正確な主張は紹介しなかったセメレディの定理について,原論文は
- E. Szemerédi, On sets of integers containing no k elements in arithmetic progression, Acta Arith., 27 (1975), 199–245.
ですが英語なので,日本語で読めるものだと
- INTEGERS『タオのセメレディ論文の§1, 2を読む』 http://integers.hatenablog.com/entry/2017/09/14/000000
- INTEGERS 『セメレディの定理の組合せ論的証明ー1』 http://integers.hatenablog.com/entry/2017/12/02/221905
が詳しいです.本論には紹介できなかった結果ですが,名古屋大の吉田裕哉氏との共同研究でセメレディの定理を拡張しました.宣伝ですが,その文献も紹介します:
- K. Saito and Y. Yoshida, Arithmetic Progressions in the Graphs of Slightly Curved Sequences, J. Integer Seq., 22 (2019), Article 19.2.1. http://z.emis.de/journals/JIS/VOL22/Yoshida/yoshida4.html
素数がいくらでも大きい項数の等差数列を含むことを証明したグリーンとタオ定理について,原論文は
- B. Green and T. Tao, The primes contain arbitrarily long arithmetic progressions, Ann. of Math. (2), 167 (2008), 481–547.
です.日本語による解説は
- INTEGERS 『等間隔に並ぶ素数を追い求めて〜グリーン・タオの定理〜』http://integers.hatenablog.com/entry/2017/09/12/000000
が詳しいです.
フラクタル幾何学については
- TED 『ブノワ・マンデルブロ フラクタルと荒さの科学』https://www.ted.com/talks/benoit_mandelbrot_fractals_the_art_of_roughness/transcript?language=ja
- K. Falconer (著),服部久美子,村井浄信 (訳) 『新しい解析学の流れ フラクタル幾何学』,共立出版,2006.
- 新井仁之 (著),『ルベーグ積分講義―ルベーグ積分と面積0の不思議な図形たち』, 日本評論社,2003.
が詳しいと思います.フラクタル幾何学を創ったマンデルブロ本人がTEDで話しているのが 『ブノワ・マンデルブロ フラクタルと荒さの科学』です.なぜフラクタルを考えたのかなどわかりやすくて,さらにとても面白いです.『 ルベーグ積分講義』はルベーグ積分の基礎からハウスドルフ次元や自己相似図形について書いてありますが,他の様々な次元の関係やフラクタル幾何学全般の話題は『フラクタル幾何学』の方が詳しいです.
今回紹介したケレティの結果:
- T. Keleti. A 1-dimensional subset of the reals that intersects each of its translates in at most a single point, Real Anal., Exchange 24 (1998/99), 843–844.
弱い等差数列とフラクタル次元の関係について:
- J.M. Fraser, K. Saito and H. Yu, Dimensions of sets which uniformly avoid arithmetic progressions. Int. Math. Res. Not. IMRN., 2017, rnx261.
- J.M. Fraser and H. Yu, Arithmetic patches, weak tangents, and dimension, Bull. Lond. Math. Soc., 50 (2018), 85-95.
宇宙の大きさについて:
- JAXA 宇宙情報センター 『宇宙の果て』http://spaceinfo.jaxa.jp/ja/edge_of_the_universe.html
グラフを描くために用いたウェブサイト:
- Wolfram|Alpha https://www.wolframalpha.com/